publications
- 물류 및 교통시스템
비선형 시계열 데이터를 활용한 도시 이동성 및 지식 추출: 코로나19 영향 규명을 위한 비교 분석
- Creator
- 유건화 연구원
- Research Type
- 개인연구

전례없는 감염병 확산은 향후 초래될 위협에 대한 예방책을 강구하는 것이 필요함을 강조한다. 본 연구에서 제안된 방법 (WTSM)은 대규모 감염병 발생 시 도시인구의 이동성 변화에 대한 패턴을 도출함으로써 도시의 기능 및 지역단위로 효과적인 정책 구상을 위해 활용 될 수 있을 것 이다. WTSM의 방법론적 함의는 다음과 같다. 일반적으로 공간 시계열 데이터는 다차원 속성을 지니고 있으며, 널리 쓰이는 Dynamic Time Warping (DTW)은 다른 길이의 stream 유사도를 측정할 수 있으나 상당한 계산복잡도가 수반되고 (O(m*n)), Symbolic Aggregate approXimation (SAX)은 DTW에 비해 계산이 빠르지만 각 구성요소를 알파벳화하는 과정에서 정보의 손실 및 왜곡을 발생시킨다. 이러한 단점을 극복하고자 본 연구에서는 효율적이고, 질적으로 높은 공간시계열 분석방법을 제안하여 이를 뉴욕의 코로나 기간 동안의 택시 데이터에 적용하였다. 클러스터링결과, 공통적으로 코로나 초기에 상당한 이동량 저하가 발생했음을 발견하였다. 뉴욕은 2020년도 12월의 첫 백신 이후, 일반 공중에게 확대됨에 따라 이동성이 점차 회복됨을 보였고, Bronx, Brooklyn, Downtown Manhattan 지역이 타 지역에 비해 회복탄성이 높은 것을 확인했다. 그러나, 시계열상으로 백신과 이동성 회복에 딜레이가 존재하는 것으로 보아, 백신도입이 즉각적인 이동회복으로는 이어지지 않았으며, 정부 및 사회의 노력 (예: 사회적 거리두기, 마스크, 백신접종 증대 등)을 통해 확진자 증가가 주는 충격 (effect of COVID-19 upsurge)은 지속되지 못하며, 변동하는 이동량 (daily fluctuating volumes)을 참고했을 때 뉴욕시민의 일상이 이동성에 큰 영향력을 발휘함을 발견했다.
- 데이터 사이언스
융합 라쏘 신호 근사기의 위발견되는 변화점의 점근적 특성
- Creator
- 유동현교수님
- Research Type
- 개인연구
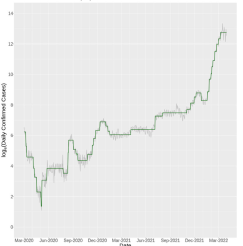
본 연구는 Fused Lasso Signal Appoximator (FLSA)에서 변화점 식별 시 위발견되는 변화점들이 점근적으로 어떠한 성질을 지니는지 이론적으로 분석하였다. 특히, 계단형태로 증가하거나 감소하는 추세를 지니는 경우에 Fused Lasso Signal Approximator에 의해 식별된 변화점 중에서는 위발견 변화점의 존재함 점근적으로 확률 1이 됨을 확인하였으며, 참 변화점 식별에 대한 일치성이 만족 되지 않음을 보인 연구결과이다. 또한, 위발견된 변화점 수에 대한 점근적 분포를 규명하여 위발견 변화점 수의 분포를 기반으로 위변화점을 최소로 포함하는 변화점 집합을 식별하는데 활용할 수 있는 연구이다. 본 연구는 시간의 흐름에 따른 변화점의 식별에 활용 가능한 연구로 소상공인의 상권 클러스터 내 업종 분류 카테고리에 따른 업체 수의 변화 추세를 식별하는데 활용할 수 있다.
- 데이터 사이언스
GAN 기반 데이터 증강 및 웨이블릿 변환을 이용한 SAR 타겟 분류 개선
- Creator
- 김재오 교수님
- Research Type
- 센터융합연구

합성 개구 레이더(Synthetic Aperture Radar, SAR)는 기상 조건과 관계 없이 지형과 표적을 관측할 수 있는 강력한 원격 탐사 기술이다. 하지만 SAR 이미지는 스펙클 노이즈(speckle noise)로 인해 표적 분류 성능이 저하되며, 레이블이 포함된 학습용 SAR이미지가 부족하다는 합계가 있다. 본 연구는 이러한 문제를 해결하기 위해 생성적 적대 신경망(Generative Adversarial Network, GAN) 기반 데이터 증강 기법과 웨이블릿 변환(Wavelet Transformation)을 활용한 노이즈 제거 기업을 결합한 새로운 학습 기법을 제안한다. 본 연구는 MSTAR(Moving and Stationary Target Acquisition and Recognition) 데이터셋을 활용하여 실험을 진행했으며, 데이터증강과 웨이블릿 변환이 SAR 표적 분류 성능에 미치는 영향을 분석하였다. 실험에서는 총 8개의 시나리오를 구성하여 기하학적 변환 기반 데이터 증강, GAN 기반 증강, 웨이블릿 변환, 그리고 이들의 조합이 성능 향상에 미치는 영향을 비교하였다. 그 결과, GAN을 활용한 데이터 증강과 웨이블릿 변환을 함께 적용했을 때 가장 높은 분류 정확도를 기록하며, 특히 학습 데이터가 제한적인 경우 성능 개선 효과가 더욱 뚜렷하게 나타났다. 본 연구는 머신러닝과 딥러닝 기법을 결합하여 SAR 표적 분류의 정확도를 향상시키는 효과적인 방법론을 제안했다는 점에서 의의가 있으며, 향후 연구에서는 다양한 SAR 데이터셋에 대한 적용 가능성 검증 및 최적의 GAN 구조 설계를 통해 보다 정교한 SAR 자동 표적 인식(ATR, Automated Target Recognition) 시스템 개발이 가능할 것으로 기대된다.
- 데이터 사이언스
가중 기댓값 최대화 알고리즘 기반 공간 데이터 분석
- Creator
- Research Type
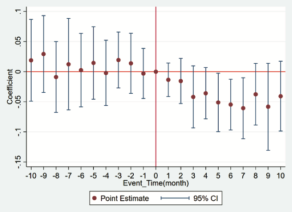
본 연구는 가중 기댓값 최대화(Weighted Expectation-Maximization, WEM) 방법을 적용하여 공간 데이터 분석을 개선하는 새로운 접근법을 제시한다. 이 방법은 다변량 데이터에서 설명 변수와 목표 변수 간의 관계를 기반으로 지역을 분류하는 데 있어 정확도 개선을 위해 오차를 최소화하도록 기존 기댓값 최대화 알고리즘에 가중치를 추가하였다. 이 연구는 지리적 정보 시스템, 도시 계획, 공공 보건 등 공간 정보가 중요한 역할을 수행하는 다양한 응용 분야에서 유용하게 적용될 수 있으며, 특히 소상공인 점포의 매출액을 예측하고 지역적 특성에 따른 매출 패턴을 보다 정밀하게 파악하는 데에도 기여할 수 있다. 부동산 거래 데이터 기반 실험을 통해 WEM 방법이 EM 방법과 비교하여 부동산 거래 데이터에서 설명 변수와 목표 변수 간의 상호작용을 더 정확히 분석하고 예측하는 데 효과적임을 보여주었다. 향후 연구에는 지리적 분포의 영향을 최소화하여 설명 변수와 목표 변수 간의 관계를 더욱 효과적으로 모형화할 방법을 연구할 계획이다.
- 데이터 사이언스
융합 라쏘 신호 근사기의 위발견되는 변화점의 점근적 특성
- Creator
- Research Type
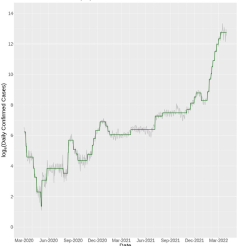
본 연구는 Fused Lasso Signal Appoximator (FLSA)에서 변화점 식별 시 위발견되는 변화점들이 점근적으로 어떠한 성질을 지니는지 이론적으로 분석하였다. 특히, 계단형태로 증가하거나 감소하는 추세를 지니는 경우에 Fused Lasso Signal Approximator에 의해 식별된 변화점 중에서는 위발견 변화점의 존재함 점근적으로 확률 1이 됨을 확인하였으며, 참 변화점 식별에 대한 일치성이 만족 되지 않음을 보인 연구결과이다. 또한, 위발견된 변화점 수에 대한 점근적 분포를 규명하여 위발견 변화점 수의 분포를 기반으로 위변화점을 최소로 포함하는 변화점 집합을 식별하는데 활용할 수 있는 연구이다. 본 연구는 시간의 흐름에 따른 변화점의 식별에 활용 가능한 연구로 소상공인의 상권 클러스터 내 업종 분류 카테고리에 따른 업체 수의 변화 추세를 식별하는데 활용할 수 있다.